
Lo smorzamento delle vibrazioni nelle macchine utensili

Uno dei requisiti fondamentali di cui si tiene conto nell’attività di progettazione di una macchina utensile è la stabilità alla vibrazione. Nel caso delle lavorazioni per asportazione di truciolo, le vibrazioni determinano la possibilità che l’utensile si avvicini e si allontani dal pezzo in lavorazione in maniera rilevante, il che determina l’insorgenza di ondulosità della superficie lavorata con conseguenti eccessive variazioni della forza di taglio, limitando così sia la durata dell’utensile stesso che della macchina.
Da un punto di vista energetico, le vibrazioni dell’utensile possono essere raggruppate in due categorie:
- vibrazioni forzate
- vibrazioni auto indotte.
Vibrazioni forzate ed autoindotte

Le vibrazioni che insorgono durante le lavorazioni per asportazione di truciolo sono associate con i carichi periodici parassiti che risultano dallo squilibrio degli alberi rotanti, dagli errori sull’accuratezza di alcuni componenti degli azionamenti o, semplicemente, dell’ingaggio ad intermittenza del pezzo in lavorazione con gli utensili a tagliente multiplo.
Tali forze periodiche forniscono l’energia meccanica per le vibrazioni forzate, determinando, come prima conseguenza, una superficie lavorata ondulata. Inoltre, se qualcuna delle componenti armoniche di tali forze è in risonanza con uno dei modi propri della struttura della macchina, la vibrazione risultante può essere piuttosto intensa. Sulla base di queste osservazioni risulta fondamentale, in fase di progettazione, la ricerca di soluzioni volte a limitare le vibrazioni forzate, unitamente alla scelta opportuna degli accoppiamenti cinematici finalizzata alla riduzione dei giochi e dei disallineamenti. Tali attività consentono di conseguire le opportune prestazioni della macchina in termini di qualità di lavorazione richiesta per un dato componente.
Le vibrazioni autoindotte insorgono nei casi in cui si ha l’aumento della velocità di rimozione del materiale; sono quindi alimentate dal processo stesso di lavorazione per asportazione di truciolo. Questa tipologia di vibrazioni viene di solito chiamata chatter e determina delle finiture di lavorazioni di qualità non accettabile, con conseguente diminuzione sia della durata della macchina che di quella dell’utensile. I tipici pattern superficiali causati dal chatter sono di seguito mostrati, nel caso di tornitura e fresatura superficiale.
Il chatter e l’analisi di stabilità
Il chatter secondo Arnold o di tipo B
Il setup sperimentale impiegato negli studi di R. W. Arnold del 1945, consisteva nella generazione del chatter ricorrendo ad un utensile da tornio montato con uno sbalzo volutamente eccessivo. La frequenza del chatter fu poi variata cambiando l’entità dello sbalzo. E’ evidente come gran parte della teoria proposta da Arnold risultò legata alla vibrazione flessionale delle travi a sbalzo, come evidenziato nell’immagine seguente.
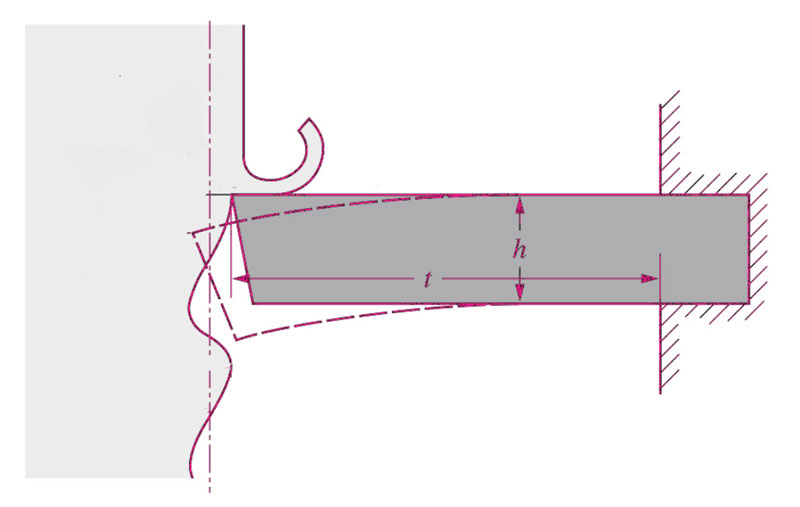
Vibrazione flessionale di un utensile da tornio.
Sulla base di questa schematizzazione, per la teoria di Arnold il chatter non comprende alcuna rigenerazione, poiché la superficie destinata alla lavorazione non presentava ondulazioni della superficie. Inoltre, la presenza di striature superficiali veniva imputata a vibrazione forzata.
Un semplice modello dinamico per questo tipo di chatter viene mostrato nell’immagine seguente.
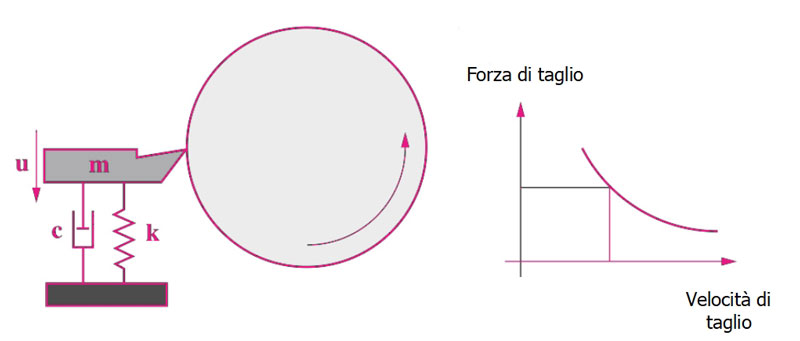
Modello dinamico per il chatter di Arnold o di tipo B
Se la forza di taglio non è costante ma può variare con la velocità, come mostrato nell’immagine precedente, allora la forza di taglio diminuisce al crescere della velocità superficiale.
Per procedere quindi allo studio dell’analisi di stabilità del chatter di Arnold, si può considerare un modello semplice ed approssimato della componente della forza di taglio nella direzione tangenziale nella forma seguente:
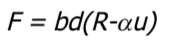
dove:
b = larghezza del taglio,
d = profondità del taglio, da cui:
bd = area della sezione trasversale indeformata del truciolo,
u = velocità superficiale istantanea del pezzo in lavorazione rispetto all’utensile,
R, α = costanti che dipendono dal materiale del pezzo in lavorazione, dallo stato e dalla geometria del tagliente.
Se l’utensile si muove su e giù si rileva (per valori realistici dell’avanzamento, della profondità di taglio e di piccole ampiezze iniziali) una variazione trascurabile nella profondità di taglio, per cui se si pone:
x(t) = spostamento dell’utensile nella direzione della forza
la forza di taglio tangenziale risulta pari a:
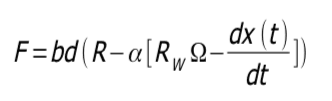
dove:
RW = raggio di lavorazione,
Ω = velocità di rotazione costante del pezzo in lavorazione.
Considerando un sistema ad 1 g. di l., l’equazione del moto è la seguente:
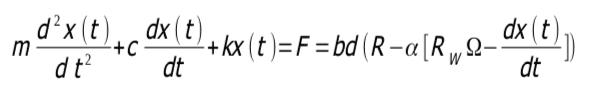
Ignorando il termine costante bd(R – aRWW)e riordinando si ottiene:
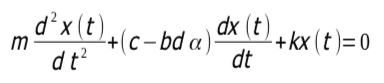
La condizione di instabilità si ha quando il termine del coefficiente di velocità diventa negativo (ad es., per smorzamento negativo). La vibrazione instabile si verificherà così quando:
![]()
Il modello del chatter di Arnold o di tipo B suggerisce che l’insorgenza del chatter dipende sia dalla lunghezza che dalla profondità di taglio, dallo smorzamento proprio dell’utensile (c) e dal fattore nell’equazione ipotizzata della forza.
Il chatter rigenerativo
Il chatter rigenerativo si può avere durante le lavorazioni di tornitura, quando una piccola oscillazione dell’utensile determina una ondulosità residua sulla superficie lavorata. Nella rivoluzione successiva del pezzo, tale superficie ondulata dovrà essere rimossa e se la larghezza di taglio è sufficientemente grande, verrà generata una ondulosità residua di ampiezza maggiore sulla superficie lavorata. Il chatter andrà quindi a rigenerarsi.
Da ciò ne deriva che, per ogni rivoluzione successiva del pezzo sottoposto a tornitura, verrà generata un’ondulosità della superficie di entità sempre più grande, determinando così una vibrazione di grandezza crescente.
Il termine chatter rigenerativo fu usato per la prima volta da Hahn nel 1952, anno in cui presentò un modello che teneva conto del contributo al chatter fornito dall’ondulosità della superficie determinata dalla vibrazione dell’utensile. Questa forma di chatter costituisce una criticità sia in ambito di produzione che progettuale, in quanto si manifesta più comunemente.
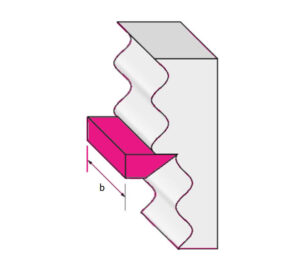
Nella figura seguente viene mostrato il moto di avanzamento radiale dell’utensile durante la lavorazione di tornitura.
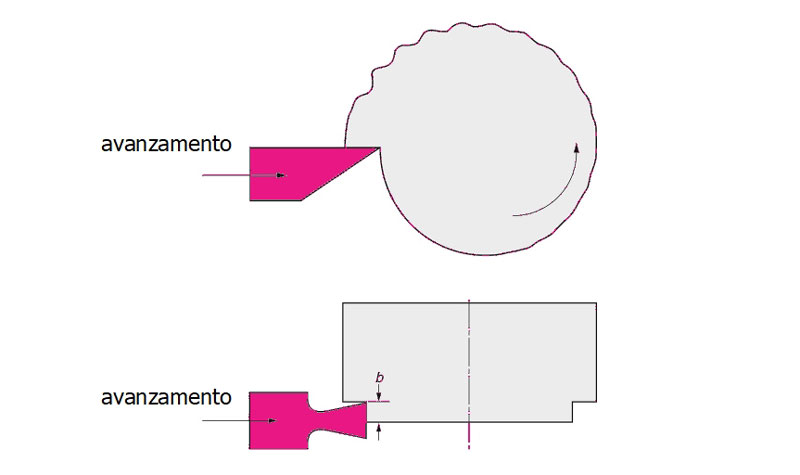
Stadio iniziale del chatter ed avanzamento dell’utensile, per una larghezza di taglio pari a b.
Esistono in letteratura diversi approcci all’analisi di stabilità del chatter rigenerativo, alcuni più orientati alla comprensione degli effetti, altri con un’impostazione matematica più spinta. In entrambe le tipologie di approccio, i modelli ottenuti costituiscono delle mere approssimazioni, le cui ipotesi vanno attentamente ed obiettivamente esaminate.
Di seguito, vengono proposti brevemente alcuni modelli maggiormente ricorrenti.
Modello della forza di taglio
Il più semplice modello della forza di taglio F prevede che questa sia proporzionale all’area della sezione trasversale indeformata del truciolo:
F = Rbd
dove:
R = coefficiente della forza di taglio,
b = larghezza del truciolo,
d = spessore del truciolo.
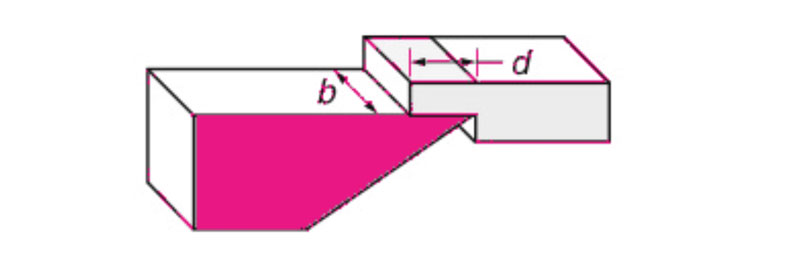
Sezione trasversale indeformata del truciolo
Sulla base della precedente relazione, la forza F non dipenderà dalla velocità di taglio, per cui verrà considerata solo la vibrazione nella direzione dello spessore del truciolo. Se lo spessore del truciolo varia, la precedente equazione fornirà l’andamento della variazione della forza di taglio, indipendentemente dalla velocità di variazione dello spessore stesso. Per quanto riguarda la direzione della forza, il modello stabilisce che essa agirà in una direzione fissata ad un angolo costante con la direzione radiale.
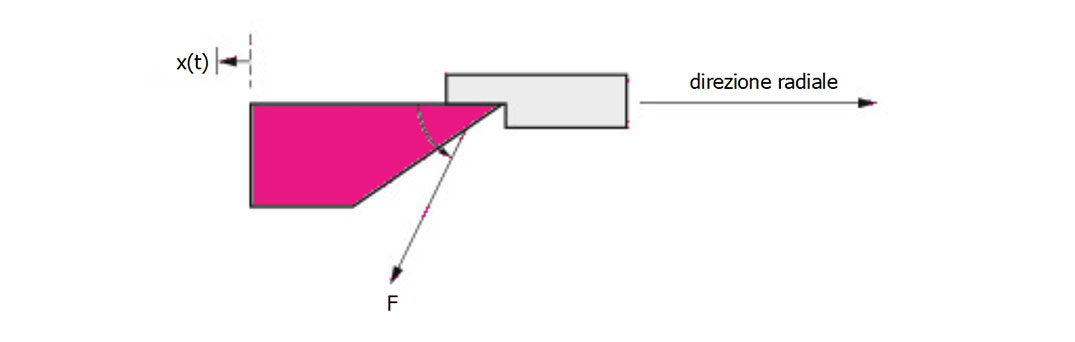
Direzione ipotizzata della forza di taglio
L’ipotesi ulteriore è che questa direzione è indipendente dalla velocità di taglio e non varia al variare dello spessore del truciolo. Vi sarà poi una forza uguale ed opposta, non mostrata in figura.
Forza oscillante istantanea
Agli inizi della ricerca sul chatter, le risorse di calcolo a disposizione erano molto limitate, per cui non era possibile condurre simulazioni nel dominio del tempo. Si ipotizzavano quindi delle condizioni al contorno stabili, con una vibrazione sinusoidale ad ampiezza costante. Queste condizioni non si verificano nella realtà, ma risultano comunque utili ed accurate per la determinazione dell’insorgenza del chatter. Le condizioni al contorno stabili vengono quindi proposte nell’immagine seguente.
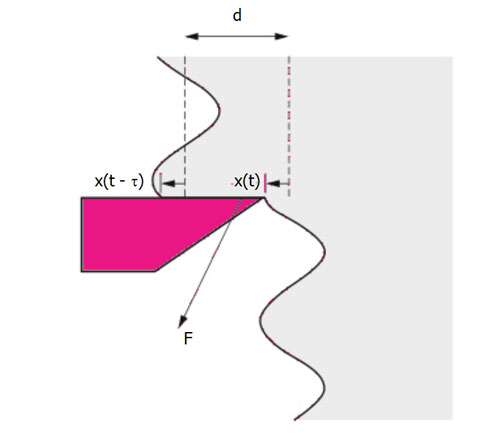
Condizioni rigenerative per vibrazione ad ampiezza costante
Si noti come nell’immagine x(t) è definita positiva se l’utensile si allontana dalla superficie di lavorazione, mentre le linee tratteggiate indicano lo spessore medio d del truciolo in assenza di vibrazione. La forza risultante F oscillante può quindi essere posta pari a:
F = Fmedia+ Fnon rigenerativa+ Frigenerativa
in particolare:
Fmedia= Rbh = costante
dove:
h = avanzamento per rivoluzione.
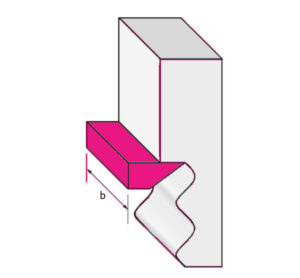
Forza non rigenerativa
Si consideri la figura a lato:
Fnon rigenerativa = – Rbx(t) (forza oscillante nell’ipotesi di assenza di ondulosità nella superficie che viene lavorata)
dove:
x(t) = spostamento dell’utensile.
Il segno – nella definizione di Fnon rigenerativa sta ad indicare che al crescere di x(t) l’utensile si allontana dal taglio, con conseguente riduzione della forza. Ciò implica che x(t) definirà l’ondulosità della superficie di taglio.
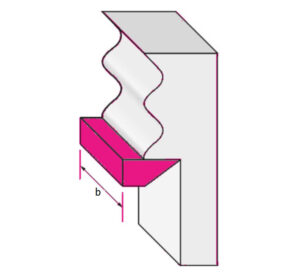
Forza rigenerativa
Si consideri la figura a lato:
Frigenerativa= Rbx(t – τ) (forza oscillante nell’ipotesi di assenza di vibrazione dell’utensile e di presenza di ondulosità sinusoidale residua della superficie, generata nella rivoluzione precedente)
dove:
x(t – τ) = ondulosità della superficie,
τ = tempo necessario per il completamento di una rivoluzione del pezzo.
Si noti come mentre valori positivi di x(t – t) incrementano lo spessore del truciolo, la forza di oscillazione aumenta.
Nella figura precedente, per il moto sinusoidale indicato la forza oscillante è in fase con l’ondulosità della superficie. Nell’immagine successiva, viene infine mostrato l’andamento della forza oscillante risultante.
Forza risultante
Si consideri, infine, la figura seguente:
La forza risultante oscillante, nel caso di moto sinusoidale ad ampiezza costante, assume la forma:
F = Rbd = Rb[h – x(t) + x(t – τ)]
Sulla base della velocità di rotazione e sulla frequenza di lavorazione, ci sarà un angolo di fase tra la vibrazione dell’utensile x(t) e l’ondulosità x(t – τ). Nel caso mostrato in figura, l’ondulosità x(t – t) è in ritardo rispetto alla vibrazione dell’utensile x(t) di 90°. Se il ritardo di fase è nullo (ad es. vibrazione dell’utensile ed ondulosità in fase), non ci sarà alcuna forza oscillante in quanto x(t) = x(t – τ) e lo spessore del truciolo (insieme alla forza di taglio) rimarrà costante per un avanzamento h.
Per una semplice analisi di stabilità al chatter, viene considerata soltanto la componente oscillante della forza poiché questa dà origine alla vibrazione ed essa stessa viene generata dalla vibrazione (rigenerazione). Perciò:
Foscillante= -Rb[x(t) + x(t – τ)]
Risposta della macchina
L’attività di progettazione delle soluzioni per lo smorzamento delle vibrazioni, dovrà tenere conto della funzione di risposta in frequenzadella macchina utensile. La funzione di risposta in frequenza da considerare è la deflessione relativa x(t) tra l’utensile ed il pezzo in lavorazione nella direzione dello spessore del truciolo, dovuta alle forze uguali ed opposte pari ad Foscillante= -Rb[x(t) + x(t – τ)], nella direzione della forza di taglio.
La funzione di risposta in frequenza verrà così definita:
G(ω) = ricettanza della macchina utensile in funzione di ω.
La ricettanza è una funzione di risposta in frequenza che lega le caratteristiche delle vibrazioni forzate del sistema (spostamenti, velocità ed accelerazioni) con la forzante unitaria alla frequenza generica. Nel piano complesso le componenti in fase e fuori fase di G(w) possono essere rappresentante rispettivamente come componente reale ed immaginaria, ottenendo:
G(ω) = GR(ω) + iGI(ω)
Se la vibrazione stazionaria ipotizzata deve continuare, allora la forza di taglio oscillante deve agire sulla struttura per determinare la vibrazione ipotizzata. Quindi, per definizione, la funzione di risposta in frequenza cercata assume la forma:
x(t) = G(ω)Foscillante= G(ω){Rb[-x(t) + x(t – τ)]}
Quindi riordinando e sostituendo:
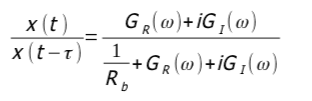
secondo Tlusty, al limite della condizione di stabilità deve essere:
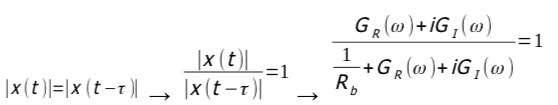
calcolando il modulo, riordinando e semplificando si ottiene:
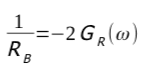
da cui si ottiene:
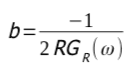
= larghezza di taglio massima nelle condizioni di stabilità.
Durante la lavorazione, la larghezza di taglio è positiva, in modo che il valore minimo di b (blimite) viene determinato dal valore massimo negativo di GR(ω) (componente in fase negativo massimo della ricettanza, GRMAX(ω)). E’ opportuno notare che la ricettanza del chatter non è stata ipotizzata per contenere un unico modo di vibrazione. Si può così misurare GR(ω) per qualsiasi macchina reale e, fatte ferme le ipotesi sin qui viste, il metodo di analisi consente di determinare la larghezza blimite per il taglio stabile, al di sotto della quale il chatter non si verificherà mai. Quindi, le macchine con caratteristiche migliorative rispetto al chatter, possono essere realizzate riducendo GR(ω).
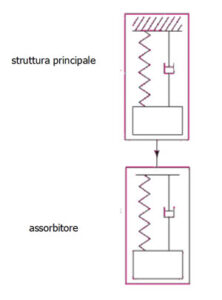
Assorbitore per una struttura con modo singolo
La progettazione degli smorzatori
L’attività di progettazione degli smorzatori, alla luce dei modelli di analisi di stabilità fin qui considerati, va condotta con lo scopo di migliorare le caratteristiche di risposta al chatter della macchina utensile.
Come primo passo fondamentale, si procede allo studio della ricettanza di ciascuno degli schemi dinamici base mostrati nell’immagine a lato.

Trave a mensola con assorbitore all’estremità

Utensile per barenatura con barra interna che sostituisce la massa dell’assorbitore e con smorzatori all’estremità

Mandrino con massa inerziale aggiunta all’estremità
Gli schemi dinamici a fianco non tengono, ovviamente, conto di tutti i limiti pratici connessi alla realizzazione pratica degli smorzatori, come (ad esempio) la non totale rigidezza del collegamento di un utensile per la barenatura o degli alloggiamenti dei cuscinetti di un mandrino.
Inoltre, le proprietà dei materiali per lo smorzamento delle vibrazioni non sono note con esattezza. Tenendo conto di queste limitazioni e degli aspetti sull’analisi della stabilità visti in precedenza, è opportuno che lo smorzamento delle vibrazioni da chatter in una macchina utensile venga realizzato tramite sistemi regolabili sul posto.
Il materiale per lo smorzamento scelto dovra poi presentare caratteristiche ben note e significative, come nel caso delle gomme butiliche.
Tale classe di gomme presentano valori di rigidezza e caratteristiche di smorzamento che crescono all’aumentare dell’area di contatto e del precarico.
Se, ad esempio, la massa dell’assorbitore è supportata da un O-ring di gomma butilica, la rigidezza può essere regolata aumentando l’area di contatto o il precarico, oppure entrambi. Nelle immagini seguente vengono presentate due soluzioni costruttive di largo impiego.
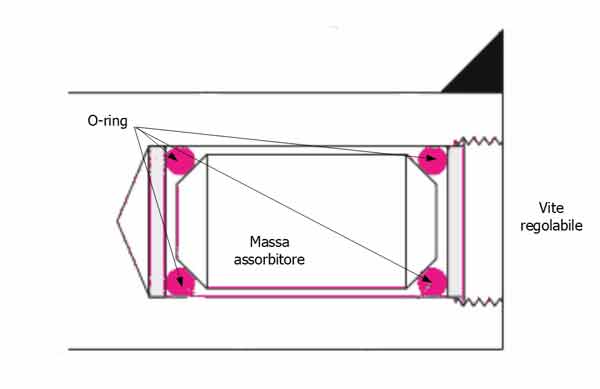
Assorbitore regolabile di un utensile per barenatura
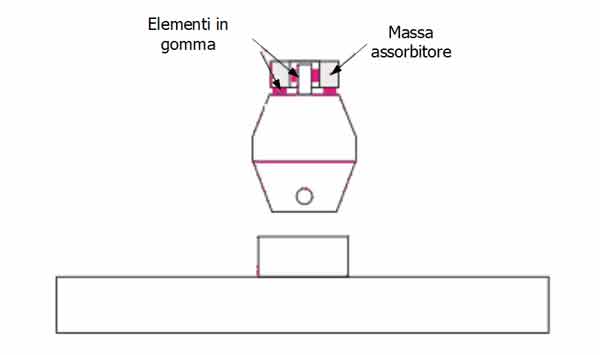
Assorbitore bidirezionale per una fresatrice
Tutto quanto visto finora costituisce una breve e sintetica rassegna delle problematiche connesse allo smorzamento delle vibrazioni nelle macchine utensili. L’analisi della ricettanza costituisce uno strumento di primaria importanza per i progettisti, che affiancheranno ad essa la scelta opportuna degli accoppiamenti cinematici con caratteristiche proprie di smorzamento delle vibrazioni e riduzione dei giochi angolari.
Un’attività complessa come la soluzione dei problemi smorzamento delle vibrazioni nelle macchine utensili, può trovare un valido supporto nei fornitori di componenti. È il caso di R+W, azienda leader nella produzione di giunti e alberi di trasmissione, in grado di mettere la sua esperienza a disposizione del progettista.
Nel settore delle macchine utensili, R+W fornisce una gamma completa di soluzioni per tutte le esigenze di trasmissione e limitazione della coppia, quali: giunti a soffietto metallico della serie BK, giunti ad elastomero della serie EK, limitatori di coppia della serie SK e giunti con allunga della serie ZA e EZ.










