
I materiali per contenere le vibrazioni negli alberi rotanti

E’ opportuno passare in rassegna le cause principali dell’insorgere delle vibrazioni negli alberi rotanti, prima di scendere in dettaglio in merito alle soluzioni progettuali più diffuse nell’ambito del contenimento delle vibrazioni, oltre che dei materiali impiegati per tale scopo.
La presenza di una massa eccentrica o squilibrata in un disco rotante, calettato su un albero, è la causa prima della vibrazione, la quale può essere considerata accettabile fino ad un certo livello. Se la vibrazione determinata dalla massa squilibrata non è più accettabile, può essere eliminata o rimuovendo la massa eccentrica o aggiungendo una massa uguale in una posizione tale da eliminare l’effetto dello squilibrio. Per stimare l’entità della massa eccentrica e la sua posizione, si ricorre a metodi sperimentali, necessari per applicare la procedura di equilibratura su indicata.
Lo squilibrio nelle macchine reali viene generalmente imputato ad irregolarità quali quelle generate dagli errori di lavorazione, dalle variazioni dimensionali di bulloni, dadi, rivetti e saldature.
Si esaminano di seguito due tecniche di equilibratura:
- equilibratura a piano singolo (o statica)
- equilibratura a due piani (o dinamica).
Indice dei contenuti
- Introduzione
- Equilibratura a piano singolo (o statica)
- Equilibratura a due piani (o dinamica)
- Cenni sulle velocità critiche degli alberi rotanti
- Il contenimento delle vibrazioni negli alberi rotanti
- Scegliere il giunto giusto per il contenimento delle vibrazioni
Equilibratura a piano singolo (o statica)
Si consideri un elemento di macchina sotto forma di disco rotante sottile (una ventola, un volano o la mola di una rettificatrice), montato su un albero. Quando il centro di massa viene spostato dall’asse di rotazione, a causa di errori di fabbricazione, si dice che l’elemento di macchina risulta staticamente squilibrato.
Il set-up tipico della prova sperimentale, usata per determinare se il disco sia equilibrato o meno, consiste nel montare il disco su un albero supportato all’estremità da due cuscinetti volventi, come mostrato nell’immagine seguente:

Set-up per l’equilibratura a piano singolo di un disco rotante.
Si pone quindi il disco in rotazione, lasciando che esso raggiunga la posizione di riposo, marcando il punto più in basso sulla sua superficie. Tale procedimento viene ripetuto più volte, marcando ogni volta nello stesso modo. Se il disco è equilibrato, i segni apposti sulla sua superficie risulteranno distribuiti in maniera random; se il disco è invece squilibrato, i segni apposti tenderanno a coincidere.
Lo squilibrio determinato con questa procedura viene chiamato squilibrio statico.
Lo squilibrio statico può essere risolto rimuovendo il materiale nel punto marcato tramite foratura, oppure aggiungendo un peso a 180° dalla posizione indicata dalla marcatura. Dal momento che l’entità dello squilibrio non è nota, la quantità di materiale da rimuovere o aggiungere deve essere determinata per tentativi e stime successive dell’errore conseguito. Questa procedura viene chiamata equilibratura a piano singolo poiché tutta la massa giace praticamente su un solo piano.
L’entità dello squilibrio viene determinata ponendo il disco in rotazione ad una data velocità w e misurando le reazioni nei due supporti, come mostrato nella figura seguente.
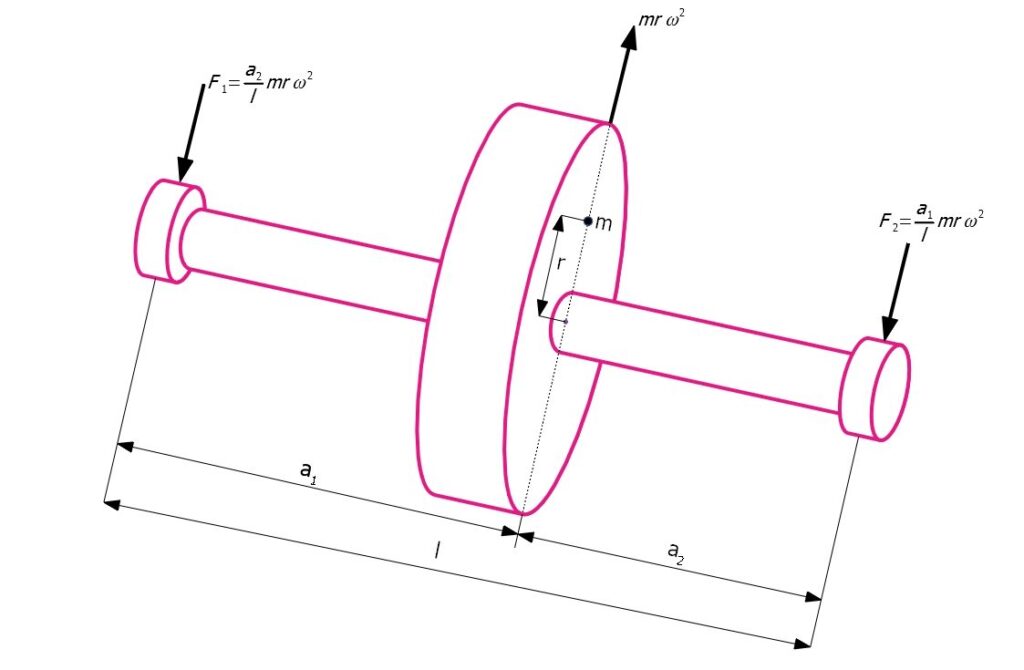
Reazioni nei supporti nell’equilibratura a piano singolo.
Dall’espressione delle reazioni indicate in figura, vengono determinati i valori di m e di r.
Un set-up sperimentale alternativo per l’equilibratura a piano singolo viene di seguito mostrato. Tale set-up prevede l’impiego di un analizzatore di vibrazioni.
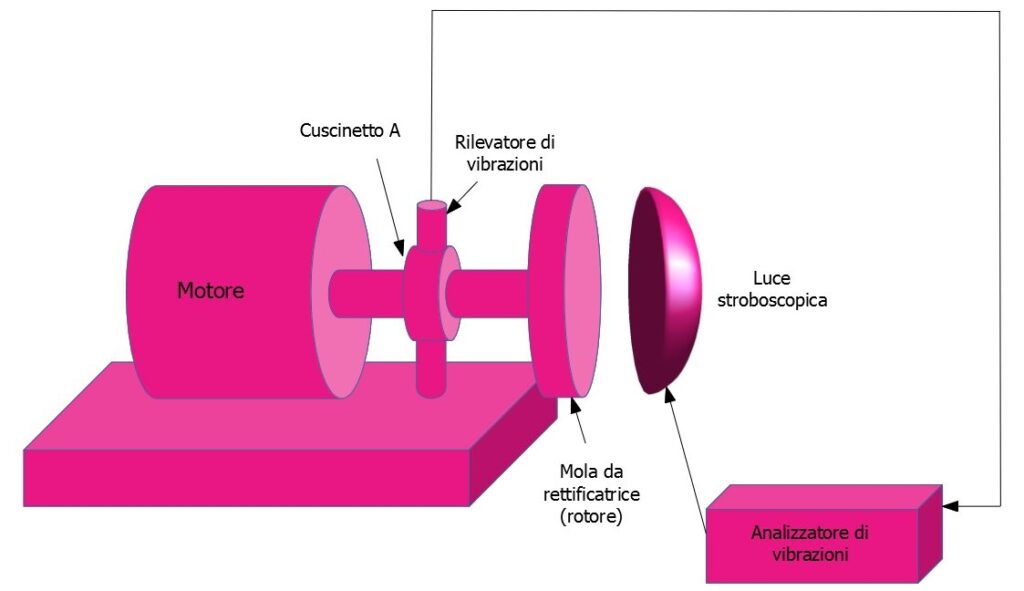
Equilibratura a piano singolo con l’impiego di un analizzatore di vibrazioni.
In questo caso il disco è dato da una mola da rettificatrice calettata su un albero rotante, il quale ha un cuscinetto montato nel punto A ed è azionato da un motore elettrico che lo fa ruotare ad una velocità angolare w. Prima di procedere alla prova, i segni di riferimento, chiamati anche segni di fase, vengono apposti sia sul rotore (disco della mola) che sullo statore, come di seguito mostrato.
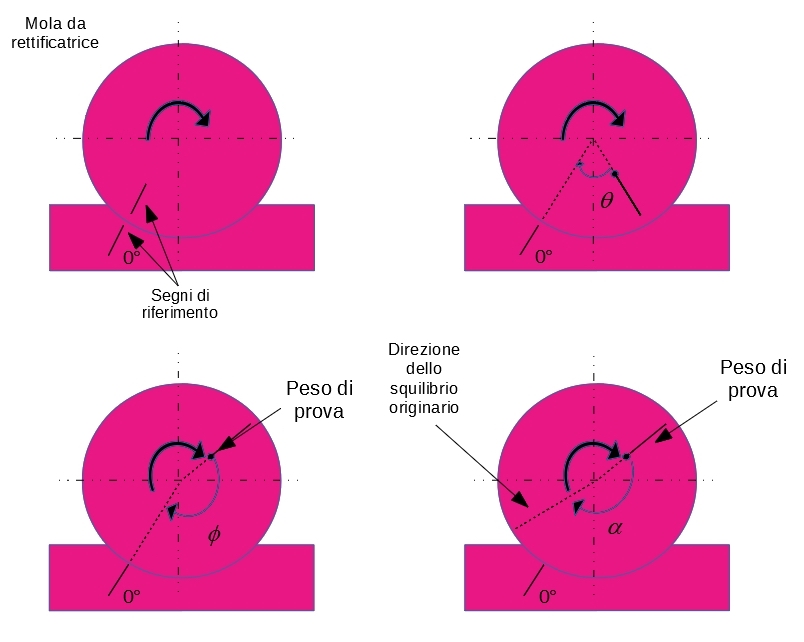
Segni di fase nell’equilibratura a piano singolo con l’impiego di un analizzatore di vibrazioni.
Un rilevatore di vibrazioni viene posizionato in contatto con il cuscinetto (come mostrato nel set-up mostrato in precedenza) e l’analizzatore di vibrazione viene settato ad una frequenza corrispondente alla velocità angolare della mola da rettificatrice. Il segnale della vibrazione (ovvero l’ampiezza dello spostamento), prodotto dallo squilibrio, può essere letto sull’indicatore graduato dell’analizzatore di vibrazione. Una luce stroboscopica viene attivata dall’analizzatore di vibrazione , alla frequenza del disco rotante. Quando il rotore gira alla velocità angolare w, il segno di fase sul rotore appare stazionario sotto la luce stroboscopica e posizionato ad un angolo q dal segno sullo statore, come mostrato nella figura precedente, per effetto del ritardo di fase nella risposta.
Sia il ritardo di fase q che l’ampiezza letta dall’analizzatore di vibrazione vengono annotati, entrambi determinati dallo squilibrio originario. Il rotore viene quindi fermato ed un peso di prova noto viene montato sul rotore, come mostrato nella figura precedente. Quando il rotore gira alla velocità angolare w, vengono annotati sia il segno di fase della nuova posizione angolare f che l’ampiezza di vibrazione, determinate dallo squilibrio combinato del rotore e del peso di prova. Tramite opportune analisi vettoriali, si determinano l’entità e la posizione della massa di equilibratura del disco, noti i valori del peso di prova e la sua direzione rispetto allo squilibrio originario.
Equilibratura a due piani (o dinamica)
Il procedimento di equilibratura a piano singolo può essere impiegato per risolvere lo squilibrio di un rotore a forma di disco, risolvendo il problema delle vibrazioni dell’albero rotante su cui è calettato. Nel caso in cui il rotore è dato da un corpo rigido allungato, come mostrato nella figura seguente, lo squilibrio può trovarsi in un punto qualsiasi lungo il rotore stesso.
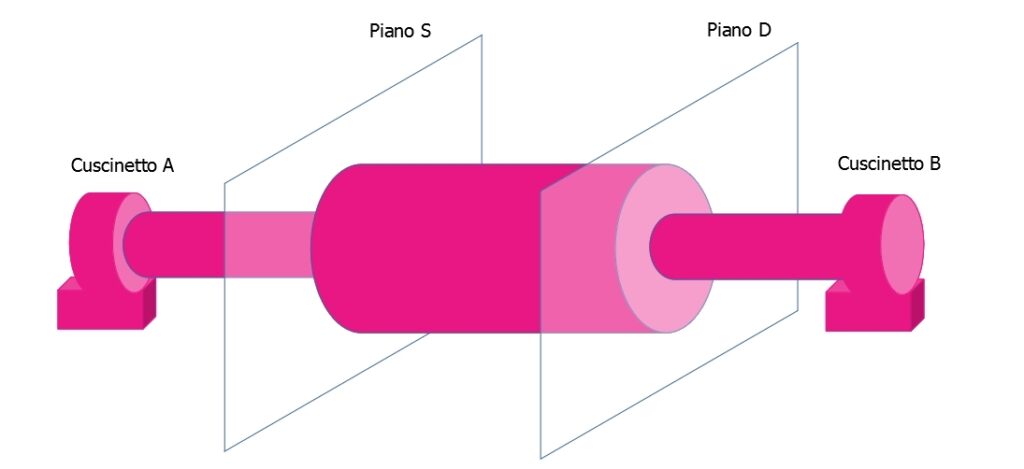
Set-up per l’equilibratura a due piani
In questo caso, è pratica comune procedere all’equilibratura del rotore aggiungendo pesi di bilanciamento su due piani qualsiasi. Per convenienza, i due piani vengono di solito scelti come passanti per le estremità del rotore, con la direzione delle loro normali parallela all’asse del rotore stesso.
Al fine di dimostrare che una qualsiasi massa squilibrata nel rotore può essere sostituita da due masse squilibrate equivalenti (in due piani qualsiasi), si consideri un rotore con una massa squilibrata m ad una distanza l/3 dall’estremità di destra del rotore, come mostrato nella figura seguente.
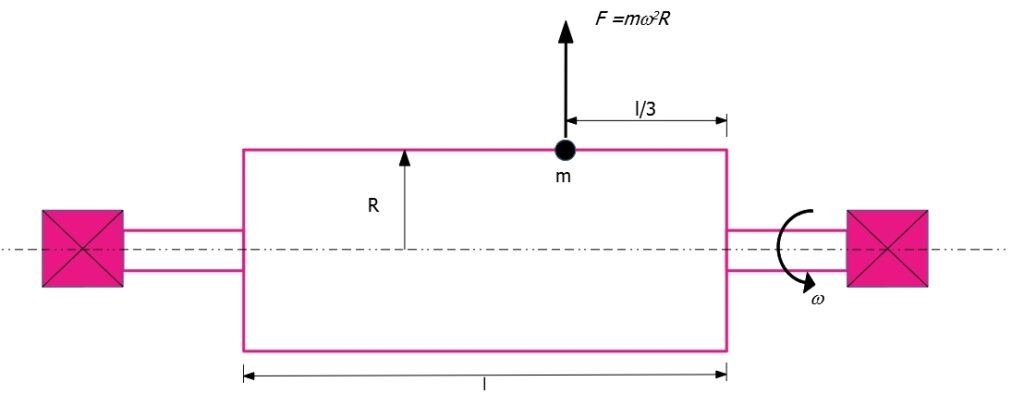
Rappresentazione della massa squilibrata nell’equilibratura a due piani.
Quando il rotore gira alla velocità angolare ω, si origina la forza F dovuta allo squilibrio mostrata in figura. La massa squilibrata m può essere così sostituita dalle due masse m1 ed m2, posizionate alle estremità del rotore, come mostrato nella figura seguente.
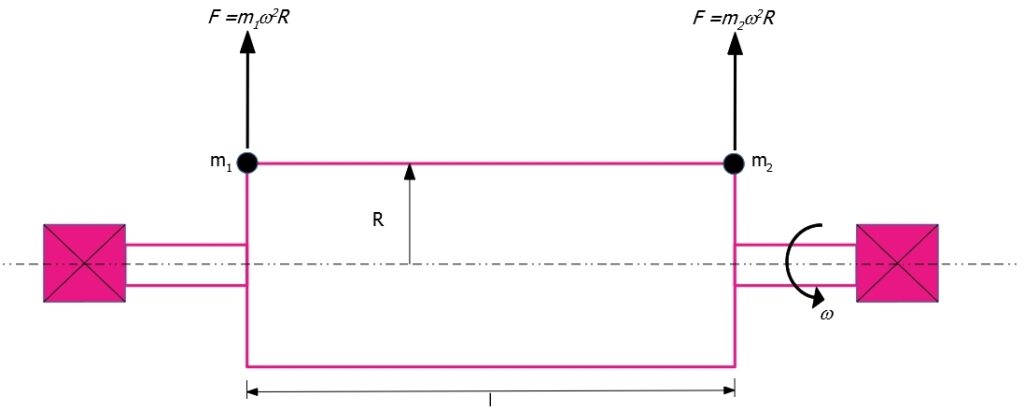
Masse squilibrate equivalenti nell’equilibratura a due piani.
Tali masse andranno ad esercitare le forze indicate nella figura precedente. Vengono anche mostrati i risultati derivanti dall’equivalenza delle forze e dei momenti, che forniscono i risultati delle masse m1 ed m2 che sostituiscono la massa squilibrata m arbitraria. Nella figura seguente, viene mostrato il procedimento di equilibratura a due piani con l’impiego di un analizzatore di vibrazioni.
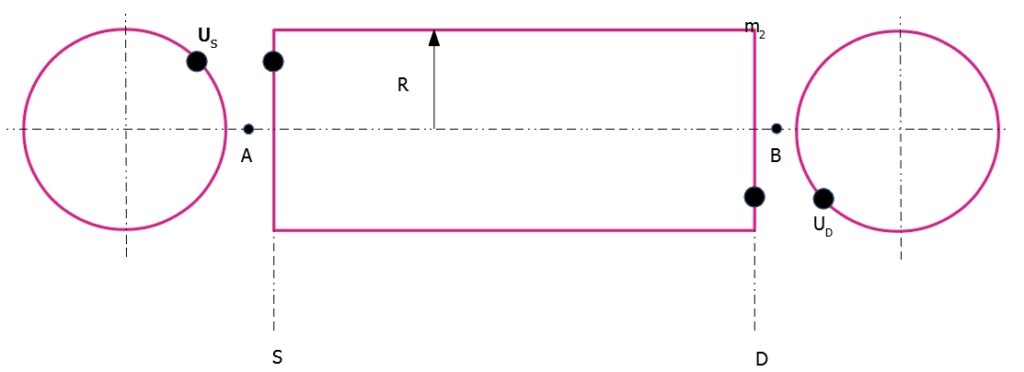
Equilibratura a due piani con l’impiego di un analizzatore di vibrazioni.
Lo squilibrio totale nel rotore viene sostituito dai due pesi squilibrati US ed UD, rispettivamente posizionati nel piano di sinistra ed in quello di destra. Quando il rotore gira alla velocità angolare w, l’ampiezza e la fase della vibrazione dovuta allo squilibrio originario vengono misurate nei due cuscinetti A e B; i risultati vengono trattati come grandezze vettoriali. Il modulo del vettore vibrazione verrà considerato come l’ampiezza della vibrazione, mentre la direzione del vettore sarà presa corrispondente al valore negativo dell’angolo di fase, osservato con luce stroboscopica, rispetto alla linea di riferimento dello statore. Con calcoli vettoriali analoghi alla procedura di equilibratura a piano singolo, si determinano le posizioni (uguali ed opposte, in termini vettoriali) dei pesi nei due piani. In base alla descrizione sintetica di queste due procedure, risulta evidente come l’equilibratura a due piani sia un’estensione di quella a piano singolo.
Sebbene i rotori ad alta velocità vengano equilibrati durante la loro produzione, risulta necessario riequilibrarli durante il loro impiego. I fenomeni principali che inducono squilibri in tali componenti sono il creep ed il funzionamento ad alta temperatura. Nella figura seguente viene mostrata un’attrezzatura per l’equilibratura a due piani del rotore di una turbina.

Equilibratura a due piani del rotore di una turbina [fonte: Cimat Balancing]
Cenni sulle velocità critiche degli alberi rotanti
Quanto esposto nelle procedure di equilibratura viste in precedenza, parte da un’ipotesi fondamentale: il rotore (formato dall’assieme albero più corpo rotante) viene considerato rigido. Tuttavia, in molte applicazioni pratiche (quali turbine, compressori, motori elettrici, pompe) un rotore pesante viene montato su un albero flessibile , leggero e supportato da cuscinetti. Ci saranno quindi squilibri in tutti i rotori, dovuti agli errori di fabbricazione.
Questi squilibri, insieme altri effetti quali la rigidezza e lo smorzamento propri dell’albero, gli effetti giroscopici e l’attrito viscoso nei cuscinetti, determineranno l’inflessione dell’albero in una maniera più o meno complicata ed a certe velocità di rotazione. Tali velocità di rotazione vengono chiamate velocità critiche. Una tipica configurazione viene di seguito mostrata.
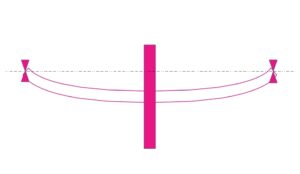
Rotore calettato su un albero flessibile.
Nell’immagine a fianco, l’albero è supportato da due cuscinetti alle estremità e su di esso è calettato in mezzeria un disco o rotore di massa m. Si ipotizza che il rotore sia soggetto ad un’eccitazione in regime stazionario dovuta allo squilibrio della massa. Sul rotore agiranno quindi forze inerziali dovute all’accelerazione del centro di massa, forze elastiche dovute all’elasticità dell’albero e forze di smorzamento interne ed esterne.
In merito a queste ultime forze è opportuno fare qualche riflessione ulteriore. Un qualsiasi sistema rotante risponde in due modi diversi alle forze di attrito o di smorzamento, a seconda che le forze ruotino insieme all’albero o meno. Quando i punti di applicazione delle forze rimangono fissi nello spazio, come nel caso delle forze di smorzamento nelle strutture di supporto dei cuscinetti (che danno origine a dissipazioni di energia), allora si avrà lo smorzamento stazionario o esterno. Se invece i punti di applicazione ruotano in maniera solidale con l’albero (come nel caso del fenomeno dell’attrito interno del materiale dell’albero stesso), si avrà lo smorzamento rotante o interno.
La velocità critica viene quindi definita come quel valore della frequenza di rotazione di un albero che eguaglia una delle frequenze naturali dell’albero stesso.
Le frequenze naturali vengono determinate tramite la soluzione delle equazioni differenziali del moto per il rotore di massa m mostrato nell’immagine precedente, in termini di equilibrio tra le forze inerziali e la sommatoria delle forze elastiche di quelle di smorzamento interne ed esterne. Quando la velocità di rotazione eguaglia la velocità critica, il rotore è soggetto a inflessioni di grande entità e le forze trasmesse ai cuscinetti possono determinare la rottura dei supporti stessi. In genere, una transizione rapida dell’albero rotante ai valori della velocità critica tende a limitare l’ampiezza di tali inflessioni, mentre una transizione lenta favorisce lo sviluppo di inflessioni di grande entità.
Le analisi più approfondite del sistema, in termini di risposta del sistema e di analisi di stabilità, reperibili in maniera estesa nella letteratura specializzata, evidenziano inoltre l’influenza dello smorzamento nella valutazione di tutte le possibili soluzioni di contenimento delle vibrazioni.
In particolare , procedendo all’analisi della risposta per un’eccitazione data da una forza armonica, l’uguaglianza tra velocità critica e frequenza naturale avviene soltanto quando lo smorzamento è zero. Inoltre, la presenza dello smorzamento incrementa il valore della velocità critica a parità di frequenza naturale e limita la risposta stessa per valori prossimi a quelli della risonanza. L’analisi di stabilità mostra come l’instabilità di un rotore flessibile sia determinata da fattori quali l’attrito interno, l’eccentricità del rotore e dai fenomeni fluidodinamici che insorgono all’interno dei cuscinetti volventi al variare dei carichi di esercizio.
Il contenimento delle vibrazioni negli alberi rotanti
In molte applicazioni pratiche è possibile soltanto ridurre le forze dinamiche che generano le vibrazioni. I principali metodi per il contenimento delle vibrazioni sono i seguenti:
- controllare le frequenze naturali del sistema ed evitare la risonanza per effetto di perturbazioni esterne;
- prevenire la risposta eccessiva del sistema , anche alla risonanza, introducendo un meccanismo di smorzamento o di dissipazione dell’energia;
- ridurre la trasmissione delle forze di eccitazione da un componente all’altro del meccanismo per mezzo di isolatori delle vibrazioni;
- ridurre la risposta del sistema tramite l’aggiunta di una massa di compensazione ausiliaria o di un assorbitore delle vibrazioni.
Nel caso degli alberi rotanti, il contenimento delle vibrazioni in relazione alle caratteristiche proprie del rotore avviene tramite il controllo delle frequenze naturali e lo smorzamento.
1. Il controllo delle frequenze naturali
Si è visto prima come il fenomeno della risonanza insorge ogni qualvolta che la frequenza di eccitazione coincide con una delle frequenze naturali del sistema. Ciò determina una rilevante entità delle inflessioni nel rotore. Queste inflessioni sono rappresentative di uno stato di tensione e deformazione assolutamente non favorevole, che può portare anche al collasso del sistema. Generalmente, la frequenza di eccitazione non può essere controllata, in quanto è imposta dai requisiti funzionali del sistema o della macchina rotante, per cui si pone l’attenzione sul controllo delle frequenze naturali come metodo per evitare l’insorgere della risonanza.
Le frequenze naturali di un sistema possono essere cambiate variandone la massa o la rigidezza. In molti casi pratici, anche la massa costituisce un requisito funzionale del sistema e perciò non può essere variata. Nel caso particolare di un rotore formato da un volano calettato su un albero, la massa del volano è prescritta dalla quantità di energia richiesta da accumulare in un ciclo. Rimane quindi la rigidezza come parametro da variare per alterare le frequenze naturali del sistema. Ad esempio, la rigidezza di un albero rotante può essere alterata variando uno o più dei suoi parametri costruttivi, come il materiale ed il numero e la posizione dei punti di supporto (cuscinetti).
2. Lo smorzamento
Lo smorzamento viene spesso tralasciato nell’analisi delle vibrazioni, al fine di semplificare la risoluzione delle equazioni differenziali del moto, per la determinazione delle frequenze naturali di un sistema. La maggior parte dei sistemi vibranti presenta, infatti, caratteristiche di smorzamento, che possono essere d’aiuto in molti casi. Come visto in precedenza, se il sistema è soggetto ad una vibrazione forzata, la sua risposta (ampiezza della vibrazione) tende a diventare alta in prossimità della risonanza in assenza di smorzamento. In ogni caso, la presenza dello smorzamento limita l’ampiezza della vibrazione. In molte applicazioni pratiche (ad esempio motori elettrici a velocità variabile, motori a combustione interna, ecc.) i requisiti del sistema prevedono il funzionamento su un intervallo di velocità per cui non è possibile evitare la risonanza in tutte le condizioni di funzionamento. A tale scopo viene introdotto lo smorzamento nel sistema per controllare la sua risposta, tramite l’impiego di materiali strutturali che hanno uno smorzamento interno elevato, come la ghisa, i laminati compositi ed i materiali sandwich.
L’incremento dello smorzamento negli accoppiamenti cinematici delle trasmissioni di potenza è affiancato all’incremento di rigidezza degli stessi, al fine di migliorare le prestazioni in termini torsionali e di compensazione dei disallineamenti. Nella Prima Conferenza Internazionale sugli Accoppiamenti Flessibili, tenutasi nel 1977 all’Università del Sussex, è stato affermato che “(…)un accoppiamento flessibile, sebbene sia relativamente più piccolo ed economico rispetto agli elementi di macchina che collega, costituisce una criticità per un qualsiasi sistema di alberi rotanti ed una buona dose di attenzione deve essere riposta nella sua scelta in fase progettuale”.
Molte soluzioni progettuali degli accoppiamenti prevedono l’uso di elastomeri per modalità di carico complesse; tali materiali presentano valori del fattore di perdita h (o loss factor, pari al rapporto tra l’energia dissipata per ciclo e la massima energia di deformazione immagazzinata) molto elevati e quindi caratteristiche di smorzamento interno favorevoli. L’elastomero più largamente usato è il poliuretano termoplastico (TPU) che presenta valori del fattore di perdita fino a 1,1. La disposizione più semplice di tali materiali è quella in cui uno strato di elastomero è attaccato ad uno elastico. In altre soluzioni, l’elastomero costituisce il core di un materiale sandwich.
Gli accoppiamenti a flessibilità torsionale costituiscono la soluzione progettuale più immediata per la riduzione dei rischi legati all’insorgenza delle condizioni di risonanza o a quella dei sovraccarichi dinamici transitori (o di entrambe). La loro influenza sulla dinamica della trasmissione è legata ad uno o più dei fattori seguenti:
- cedevolezza torsionale;
- smorzamento;
- non linearità della caratteristica di deformazione.
Tali accoppiamenti conseguono la riduzione della rigidezza torsionale della trasmissione e, di conseguenza, la variazione delle sue frequenze naturali. Se una condizione di risonanza si verifica prima dell’istallazione (o della sostituzione) dell’accoppiamento, la variazione della frequenza naturale dovuta all’impiego di un accoppiamento ad alta cedevolezza torsionale può eliminare la risonanza, così i carichi dinamici e le vibrazioni torsionali verranno sostanzialmente ridotte.
La capacità efficace di smorzamento di una trasmissione può essere incrementata se i suddetti accoppiamenti sono ad alto smorzamento, qualora non vengano usati smorzatori speciali. Quando lo smorzamento di un sistema viene incrementato senza variare la sua rigidezza torsionale, l’ampiezza delle vibrazioni torsionali viene ridotta nelle zone di risonanza ed in quelle prossime alla risonanza. Lo smorzamento incrementato è particolarmente consigliato quando c’è un ampio spettro di frequenze di disturbo che agiscono sull’azionamento (ad esempio, gli azionamenti delle macchine universali). L’effetto di uno smorzamento incrementato in un accoppiamento a flessibilità torsionale è evidente nel gruppo trasmissione delle fresatrici.
L’introduzione di non linearità nel sistema della trasmissione consente l’allontanamento automatico dalla risonanza ad una frequenza di eccitazione fissata, tanto più che è maggiore la variazione relativa della rigidezza complessiva del sistema, durante la fase in cui la deflessione torsionale uguaglia l’ampiezza di vibrazione. Ad esempio, quando lo smorzamento è basso, una variazione relativa della rigidezza di un fattore 1.3 riduce l’ampiezza di risonanza di circa 1.7 volte, ma una variazione relativa della rigidezza di un fattore pari a 2 riduce l’ampiezza di risonanza di 1.85 volte. Quindi, gli accoppiamenti non lineari a flessibilità torsionale possono essere molto efficaci nelle trasmissioni dove possono insorgere vibrazioni torsionali ad alta intensità e dove la cedevolezza del giunto costituisce gran parte della cedevolezza complessiva.
Di seguito vengono mostrati due tipi di giunti a flessibilità torsionale.
- Giunto flessibile Dynaflex® della serie LCD [fonte: Lord]
- Giunto flessibile Bibby, con particolare del funzionamento del corpo flessibile circonferenziale (fonte: https://www.bibbyturboflex.com/)
Il giunto Dynaflex® LCD viene principalmente usato nei collegamenti albero – volano, mozzo-volano, albero-albero ed albero flottante. L’impiego di questi giunti risulta comunque limitato, in quanto risultano rigidi nella direzione di compensazione dei disallineamenti che è richiesta in molte applicazioni. Per questo motivo, vengono usati in maniera più diffusa i giunti polivalenti, anche al posto di quelli a flessibilità torsionale e con una minore o maggiore capacità di compensazione dei disallineamenti.
La rigidezza torsionale costituisce, infatti, l’indicatore principale della capacità di carico in condizioni di esercizio, sia per i giunti a flessibilità torsionale che per quelli polivalenti.
Scegliere il giunto giusto per il contenimento delle vibrazioni
Un’attività complessa come la soluzione dei problemi di contenimento delle vibrazioni degli alberi rotanti, può trovare un valido supporto nei fornitori di componenti. È il caso di R+W, azienda leader nella produzione di giunti e alberi di trasmissione, in grado di mettere la sua esperienza a disposizione del progettista. In tutti i settori in cui il contenimento delle vibrazioni degli alberi rotanti costituisce una criticità progettuale, R+W fornisce una gamma completa di soluzioni per tutte le esigenze di trasmissione: in particolare, i giunti di precisione ad elastomero della serie EK, che permettono lo smorzamento delle vibrazioni in totale assenza di gioco angolare.












