
La sintesi cinematica di una pinza robotica

La realizzazione del meccanismo di una pinza robotica è un’attività di progettazione con aspetti di grande interesse, tuttora oggetto di diverse attività di ricerca in corso presso le più importanti università e centri di eccellenza internazionali.
L’approccio di base a tale attività, fa riferimento agli studi pubblicati nel 1998 dal Dr. Jay Lee, docente al College of Engineering and Applied Science dell’Università di Cincinnati, nonché fondatore di diversi consorzi di ricerca di livello mondiale. Il Dr. Lee è considerato tra i principali innovatori in ambito di Smart Manufacturing e tra i pionieri riconosciuti dell’ Industria 4.0
Gli studi del Dr. Lee hanno fissato alcuni punti chiave, che verranno sinteticamente proposti.
Introduzione al problema
Lo scopo principale della sintesi cinematica di una pinza robotica, componente il gruppo terminale di un robot antropomorfo (maggiormente diffuso in ambito industriale, affiancando in alcuni casi anche quelli cartesiani), consiste nella determinazione dei gradi di libertà del relativo meccanismo e nella successiva analisi della complessità strutturale dello stesso.
Per conseguire tali scopi, è fondamentale ricorrere all’applicazione di due discipline:
- la sintesi cinematica;
- la teoria dei grafi.
1. Sintesi cinematica
La sintesi cinematica è una branca della cinematica che ha lo scopo di individuare dei metodi per l’ideazione di meccanismi, destinati all’ottenimento di date prestazioni e funzionalità.
La sintesi cinematica esamina la generazione di movimenti (successione di un numero finito di posizioni di un componente del meccanismo), la generazione di traiettorie (relative ad un punto individuato su un componente del meccanismo) e la generazione di funzioni (ovvero di legami tra il moto di due componenti, secondo una relazione prefissata).
Nel caso in particolare della sintesi cinematica di una pinza robotica, spesso viene risolto un problema di cinematica diretta, dovendo procedere al calcolo della posizione (ed anche dell’orientazione, della velocità e dell’accelerazione) di un attuatore di estremità, noti i valori delle variabili di giunto. La determinazione dei valori di tale variabili viene invece determinata grazie alla cinematica inversa, noti i valori relativi ad un dato percorso di un’attuatore di estremità. Tale disciplina è alla base degli studi di ridondanza (ovvero delle differenti possibilità di realizzazione dello stesso movimento), della prevenzione delle collisioni e delle singolarità. Noti i risultati degli studi della cinematica, grazie alla dinamica diretta si possono determinare le accelerazioni note le forze applicate; tale disciplina è alla base delle implementazioni usate nelle simulazioni numeriche. La dinamica inversa, infine, consente il calcolo delle forze di attuazione data una determinata accelerazione di un attuatore di estremità e viene usata per il miglioramento degli algoritmi di controllo.
2. Teoria dei grafi
La teoria dei grafi è una disciplina trasversale ad altre di primaria importanza, quali la matematica, l’informatica e la geometria combinatoria; quest’ultima è quella maggiormente impiegata non solo nell’attività di progettazione di una pinza robotica, ma anche a livello più generale, qualora sia necessario implementare algoritmi di AI in ambito robotico.
Questa teoria si occupa dello studio dei grafi, oggetti discreti che consentono la schematizzazione delle interazioni tra le componenti dei meccanismi in maniera univoca, permettendone sia l’analisi in termini quantitativi che la traduzione degli stessi in algoritmi implementabili.
La geometria combinatoria si occupa dello studio di insiemi finiti e numerabili di oggetti, legati tra loro da relazioni di appartenenza e di ordine. La teoria dei grafi risolve anche problemi di geometria topologica, ovvero di quei problemi relativi alla deformazione di figure geometriche senza l’insorgenza di strappi, sovrapposizioni ed incollature. Precursore di tutte queste discipline è stato il celebre matematico svizzero Eulero.
E’ immediato apprezzare come l’impiego di tali discipline per lo studio dei meccanismi sia di fondamentale importanza, specie per la sempre più crescente attenzione verso il Digital Manufacturing, che prevede sia l’impiego esteso di sistemi informatici integrati che attività di progettazione ottimizzate in termini di risorsa temporale.
Inoltre, tali discipline forniscono una visione ampia, anche a livello concettuale, delle problematiche relative alla corretta progettazione degli accoppiamenti cinematici.
Partendo quindi dalla fine degli anni ‘90, la progettazione della pinza robotica ha costituito il fulcro di tutte le attività di ricerca che hanno portato al potenziamento delle linee di produzione automatizzate nel settore manifatturiero. Tale innovazione ha delineato, sin da subito, gli attuali scenari in cui tali sistemi operano e che hanno portato alla sostituzione, quasi completa, degli operatori nei reparti di assemblaggio e di movimentazione di materie prime e semilavorati.
Di seguito viene mostrato un moderno robot antropomorfo:

Robot antropomorfo (fonte : https://www.kuka.com/)
La progettazione di tali sistemi robotici presenta, comunque, altre criticità, specie relative alle fasi preliminari. I livelli attuali di progresso e di sviluppo del settore, rendono disponibile una scelta di componenti semplicemente impensabile fino a pochi decenni fa. Tale vastità di scelta, unitamente alla disponibilità di software CAE capaci di importare modelli 3D già preimpostati e forniti dalle case produttrici stesse, rende la progettazione di un meccanismo robotico estremamente più agevole, rispetto a pochi decenni prima. Questo fattore, però, spesso spinge il progettista al ricorso a topologie di meccanismo preesistenti, rischiando di perdere di vista gli aspetti di ottimalità del sistema.
Tipologie di meccanismi delle pinze robotiche
I meccanismi tipici di una pinza robotica vengono classificati come di seguito:
- Sulla base delle dita di presa si distinguono:
- pinze a due dita;
- pinze a tre dita;
- pinze a dita multiple.
- Sulla base del numero di pinze montate sul terminale del robot antropomorfo, si distinguono:
- a pinza singola;
- a pinza doppia;
- a pinza multipla.
- Sulla base del cinematismo impiegato, si distinguono:
- a sistema articolato;
- a pignone/cremagliera;
- a camme;
- a vite;
- a cinghia e puleggia.
- A presa pneumatica o magnetica
- Altri tipi speciali.
Di seguito vengono mostrate una moderna pinza a 4 griffe (ad azionamento pneumatico ed autocentrante), una pinza a presa pneumatica ed una a presa magnetica:

Pinza robotica autocentrante, Pinza a presa pneumatica, Pinza a presa magnetica (fonte: https://schunk.com)
Le due ultime tipologie di pinze mostrate sono ricorrenti principalmente in configurazioni robotiche di tipo cartesiano.

Pinza collaborativa a due griffe (fonte: https://schunk.com)
Le attuali innovazioni nel settore dell’automazione comprendono anche l’introduzione della robotica collaborativa (cobot), nella quale l’interazione uomo-robot è fondamentale al mantenimento della produttività di ben determinate aree di lavoro (workspace). L’esigenza principale della robotica collaborativa è quella di garantire la sicurezza dell’operatore che interagisce con la pinza del robot stesso. A tale scopo è stata concepita la prima pinza collaborativa, di seguito mostrata, che presenta una particolare ingegnerizzazione non solo in termini di azionamenti e sensori di prossimità ma anche di cura nei materiali anticollisione e di segnalazione dello stato di funzionamento:
Il livello di progresso sempre più crescente della manipolazione automatica, alla luce delle prerogative di collaboratività su esposte, prevede un’attenzione verso la scelta degli accoppiamenti cinematici tali da garantire elevati livelli di precisione nell’attuazione e di limitazione della coppia. Saranno quindi ottimali quegli accoppiamenti con elevata rigidità torsionale, capacità di compensazione dei disallineamenti, mentre la limitazione della coppia assume un’importanza rilevante specie nei contesti su indicati in cui la movimentazione deve rispondere alle vigenti norme di sicurezza nelle interazioni con l’operatore, come gli standard DIN EN ISO 10218-1, DIN EN ISO 10218-2 e DIN EN ISO/TS 15066.
Sintesi cinematica del meccanismo di una pinza robotica
L’attività di progettazione dei meccanismi, basata sulla separazione della struttura dalle sue funzionalità, fu proposto nel 1979 da un gruppo di ricercatori della General Motors. La struttura cinematica può quindi essere descritta in maniera essenzialmente sistematica, imparziale, come funzione del grado di libertà del meccanismo, della tipologia del moto richiesto e di un ulteriore parametro che rappresenti l’indicazione della complessità del meccanismo stesso.
Ciascuna struttura così ottenuta può essere quindi disegnata e validata rispetto ai requisiti funzionali del meccanismo da realizzare. Inoltre, possono essere concepiti (contemporaneamente) diversi meccanismi potenzialmente validi, fino al raggiungimento di una scelta progettuale finale.
Gran parte dei meccanismi rispettano l’equazione generica dei gradi di libertà:
l = m (L – c – 1) + F
dove:
l = numero dei gradi di libertà;
m = 3 (moto piano o sferico);
m = 6 (moto spaziale);
L = numero aste;
c = numero coppie cinematiche;
F = somma dei gradi di libertà relativi rilasciati dalle coppie cinematiche.
Passando poi all’applicazione della teoria dei grafi, si procede inizialmente alle assegnazioni seguenti:
Aste del meccanismo L → vertici del grafo v;
Coppie cinematiche c → lati del grafo e;
si definisce poi:
NAI = Numero di Anelli Indipendenti
l’equazione generale dei gradi di libertà assume così la forma:
l = m (v – e – 1) + F
con significato analogo dei simboli ricorrenti. Inoltre risulta:
NAI = c – L + 1
per cui:
F = l + NAI
E’ interessante notare la forma assunta dalle precedenti relazioni, nel caso in cui nel meccanismo di una pinza robotica vengano impiegate coppie di ruote dentate. Con le opportune sostituzioni si ottiene:
L = l + 1 + NAI
c = L + 2 * NAI
definendo poi:
cG = NAI = numero di coppie di ruote dentate;
cR = l + NAI = numero dei perni in comune.
La maggior parte delle pinze robotiche sono realizzate con meccanismi ad anello aperto, le cui strutture sono in genere più semplici di quelli ad anello chiuso.
Le coppie cinematiche più ricorrenti negli schemi progettuali delle pinze robotiche sono i perni, le coppie prismatiche, le coppie di ingranaggi, le coppie elicoidali e la coppia vite – madrevite.
Si consideri, ad esempio, la seguente schematizzazione di una pinza robotica a due griffe con dita di presa standard:
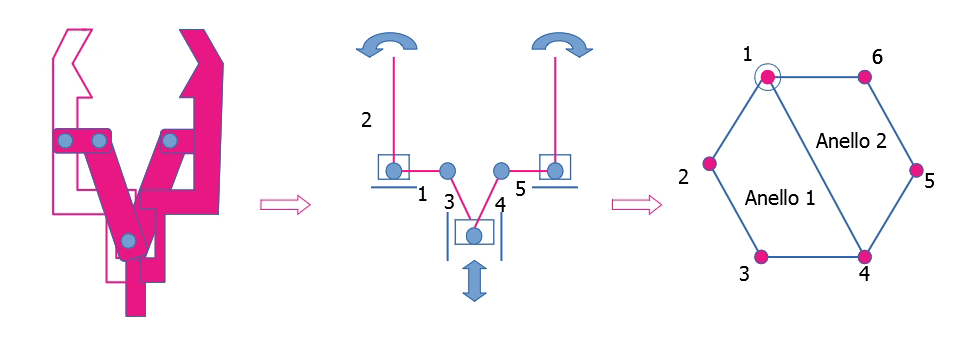
Schematizzazione di una pinza robotica a due griffe e grafo associato.
Applicando le precedenti relazioni si ottiene:
L = numero di aste = 6;
c = numero di coppie cinematiche = 7;
m = 3 (meccanismo piano).
→ l = 3 (6 – 7 – 1) + 7 = 1; NAI = 7 – 6 + 1 = 2.
Sulla base di questo semplice esempio (comunque costituente lo step fondamentale dell’attività di progettazione di una pinza robotica), è immediato apprezzare l’importanza comunque rilevante della sintesi cinematica nello sviluppo di pinze robotiche a griffe multiple.
Inoltre, l’apparente semplicità di quest’approccio non deve ingannare circa le reali difficoltà incontrate nelle ricerche condotte negli ultimi cinque anni, specie nell’estensione della fase di studio successiva alla sintesi cinematica che è la sintesi strutturale.
L’obiettivo principale della sintesi strutturale di una pinza robotica consiste nella determinazione degli scenari topologici per il conseguimento di un afferraggio ottimale (grasping).
Uno degli ambiti di ricerca più recenti riguarda, infatti, la realizzazione di pinze robotiche a dita di presa multiple con specifiche di afferraggio con destrezza. Tali soluzioni stanno gradatamente portando verso la realizzazione di pinze robotiche ad azionamento completo, antropomorfe e con spiccate caratteristiche biomimetiche.
Un risultato interessante è quello proposto nel 2012 dall’Harvard Biorobotics Lab, di seguito rappresentato:
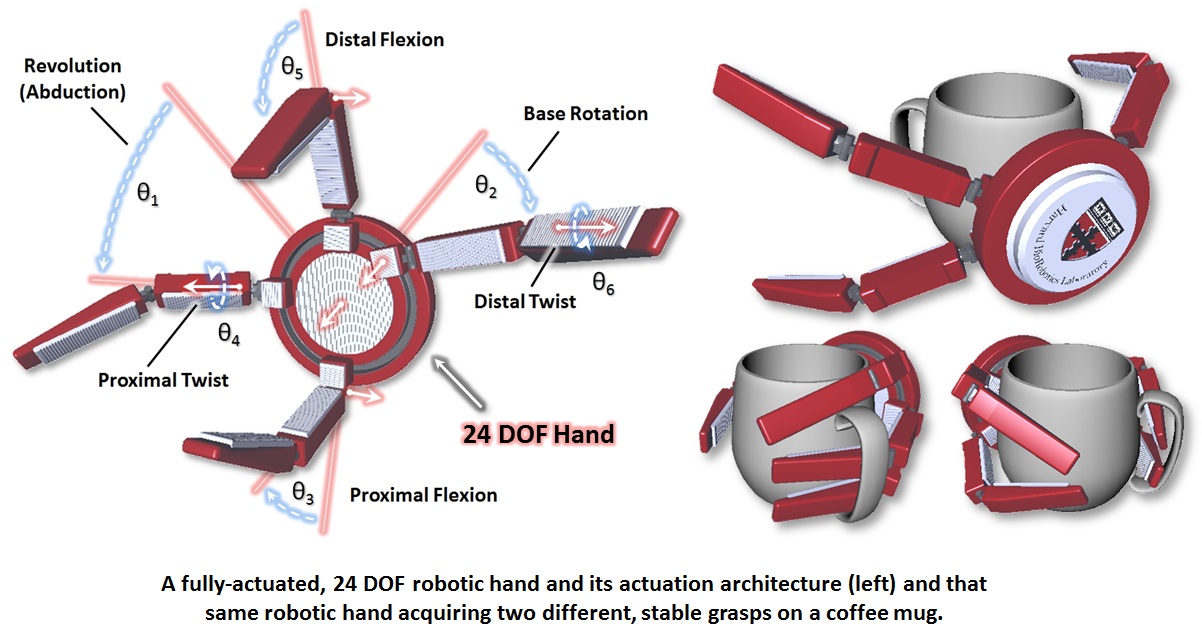
Risultati degli studi di ottimizzazione numerica di una pinza a dita di presa multiple sotto-attuata
(fonte: http://biorobotics.harvard.edu/robotic_hand_optimization.html)

Particolare delle dita di presa biomimetiche, ispirate alle zampe adesive del gecko.
Nella tipologia di pinza robotica su mostrata, sono previste soluzioni per l’attuazione ancora troppo complesse e costose per una loro applicazione su larga scala. Le pinze robotiche di questo tipo sono sotto-attuate, ovvero sono quelle pinze in cui gli attuatori classici sono sostituiti da componenti passivi realizzati con meccanismi cedevoli (compliant mechanism) che (sebbene potranno costituire, a breve, una valida e meno costosa alternativa rispetto, ad esempio, agli azionamenti induttivi) sono tuttora molto difficili da trattare ai fini del conseguimento delle prerogative di adattabilità e qualità del grasping per i manipolatori.
Parallelamente a quest’approccio ve ne sono altri basati sul ricorso più spinto alla biomimesi. In queste ultime settimane, presso l’Università della California a San Diego viene presentata una ricerca riguardante l’imitazione delle dita adesive delle zampe di un gecko.
Il ruolo del fornitore di componenti
Un’attività complessa come la progettazione in ambito robotico, può trovare un valido supporto nei fornitori di componenti. È il caso di R+W, azienda leader nella produzione di giunti e alberi di trasmissione, in grado di mettere la sua esperienza a disposizione del progettista.
Nel settore della robotica, R+W fornisce una gamma completa di soluzioni per tutte le esigenze di trasmissione e limitazione della coppia, quali: giunti a soffietto metallico della serie BK, giunti ad elastomero della serie EK, limitatori di coppia della serie SK e giunti con allunga della serie ZA e EZ.










